МЕТОДЫ ОПРЕДЕЛЕНИЯ СТАТИСТИЧЕСКИХ ОЦЕНОК

Для получения зависимостей, по которым на основании выборочных значений (xi, х2, …, х„) могут быть

найдены оценки ©ж искомых параметров &х, существует несколько методов. Один из наиболее общих методов — метод максимума правдо­подобия, разработанный Р. Фишером. Этот метод позволяет получать состоятельные несмещенные или малосмещенные эффективные оценки с законом распределения, асимптотически стремящимся к нормальному при увеличении объема выборки.

Суть метода максимального правдоподобия сводится к следующему. Пусть заданы непрерывная случайная величина X с плотностью f(x, ©я), зависящей от параметра (вектора параметров) 0Т, и выборка (х4,

х2….. хп) как результат п независимых испытаний. Найдем условную

плотность вероятности выборки (xi, х2, …, хп) при фиксированном зна­чении параметра ©ж, т. е. составим функцию правдоподобия:

Цхи х2, …, хп, ©д) — f(xі, ©я)/(х2, ©Д… f(xn, Qx). (5.6)

Так как значения xir х2, …, хп и вид плотности f(x, 0Ж) известны, то функция правдоподобия зависит только от величины ©ж. Сущ­ность этого метода заключается в том, что в качестве оценки макси-

мального правдоподобия 0Ж параметра ©ж выбирают такое значение 0Ж, которое обращает функцию правдоподобия (5.6) в максимум. Другими словами, отыскивается такое значение 0Ж, при котором макси­мальна вероятность получить именно такую выборку (л’ь х2, …, хп), которая имела бы место в испытаниях. Если функция (5.6) имеет един­ственный максимум в области допустимых значений 0Ж (далее будем полагать, что это условие выполнено), то для его определения необхо­димо решить уравнение правдоподобия

Если @ж — вектор, то получим систему уравнений правдоподобия. Обычно используют логарифмическую функцию правдоподобия InL и для определения оценок ищут ее максимум, решая уравнение

(5.8)

Естественно, что одно и то же значение 0Ж обращает функции Ц0Ж) и 1пЕ(0ж) в максимум, если он существует.

Когда случайная величина Л’ дискретна и может принимать значе-

ния £i, |2, …. Si. …. а ти т2, …, ти…,тг — частоты этих значений

Г

В выборке, Причем 2тг= п и ВЄр(Х = Si ) ~ Pi(®x)> ТО фуНКЦИЯ

i=l

правдоподобия

(5.9)

Определим оценки максимального правдоподобия параметров би­номиального и нормального распределений, а также распределения Пуассона.

В биномиальном распределении (см. табл. П.1) параметр Р — вероятность появления события в каждом из п независимых испыта­ний, заканчивающихся появлением или непоявлением события.

Вероятность получения в п испытаниях ровно т отказов, если ве­роятность успеха в одном испытании Р определяется выражением

вер (т= т) = ———— ——— Р(п~т) (1 —Р)т, (5.10)

(п — т) ! ml

гдет — случайная величина числа отказов, наблюдаемых в п испыта­ниях.

На основании (5.9) функция правдоподобия

Ь[т, Р) = — —- (5.11)

[n — ту. т

/ч

Опуская постоянный множитель п/(п — т) т, не влияющий на

положение максимума функции (5.11), логарифмируя и беря частную производную по Р, получаем:

lnL(m, Р) — (п — m)laP + mln(l — Р);

Л Л

5 In L п — т т

дР " ~Р 1 — Р

Уравнение правдоподобия (п — т)1Р — т/(1 — Р) = 0 имеет одно решение, обращающее L(m, Р) в максимум:

Р = 1 — min. (5.12)

Таким образом, выражение (5.12) — искомая оценка максималь­ного правдоподобия параметра Р. Оценка (5.12), зависящая от выбо-

л

рочного значения т, имеет распределение с математическим ожиданием Р и средним квадратическим отклонением

с [p]=0p = -|/p(l_P)/n« V’P{ — Р)/{п — 1). (5.13)

Как известно, при больших пиР< 0,10 или 1 — Р < 0,10 бино­миальное распределение сходится к более простому распределению Пуассона (закон редких событий). Для этого закона [см. табл. П.1, П.5 — П.7 и выражения (2.1), (2.2)] вероятность в п независимых ис­пытаниях наблюдать ровно т раз данное событие зависит только от параметра а:

Р = ат е~°/т. (5.14)

Найдем оценку максимального правдоподобия для параметра а. В соответствии с (5.14) и (5.9) логарифмическая функция правдопо­добия

/ / lnZ.(m, а) = тпа — а — ln(ml). (5.15)

Дифференцируя (5.15) по а, получим уравнение правдоподобия т/а — 1=0, откуда оценка максимального правдоподобия

а = т. (5.16)

Покажем, что при малых значениях а оценка (5.16) имеет X2 (хи — квадрат-распределение (см. табл. П.1 и П.8) со средним квадратиче­ским отклонением

crfa] = оа = v а т Vа, (5.17)

а при больших значениях а распределение оценки (5.16) близко к нор­мальному.

Нормальное распределение с плотностью (2.96) (см. табл. П.1—П.4) определяется параметрами тх и о2х. Оценки максимального правдоподо­
бия тх и о можно найти по функции правдоподобия, которая в соот­ветствии с (2.96) и (5.6) записывается следующим образом:

(*г~т* )2

П п ‘

/ 2л Г"! 1 2a*

£, (Х^, х2,… , Xj, … , Хп, Під., Ох) д ^ ,———- ®

п ’S (*І — /И. г)2-

<=1 аж у 2л

т-

умножая левую и правую части на о*> 0Г

В соответствии с (5.8) и (5.18) уравнения правдоподобия принимают вид

(5.19)

а из второго имеем

(5.20)

Можно показать, что оценка (5.20) несколько смещена. Несмещенная оценка дисперсии

2 і хп L Л )

а =———— > , и, — тх1 .

* п — 1 Ju

і=і

Если вместо оценки тх известно истинное значение тх, то несме­щенная оценка дисперсии

(5-22)

1=1

Оценка (5.19) как сумма нормально распределенных случайных выборочных значений xt имеет нормальное распределение с математи­ческим ожиданием тх и дисперсией 02т = 02х/п, если известно истин-
not’ значение ax. Если же вместо истинной величины а2,, найдена толь­ко ее оценка, то используют распределение Стьюдента (см. табл. П.1 и

_________________________________________________________________________________________________________________ /X —— /X

П.9), которому подчиняется случайная величина (тх — гпх)г п/ох.

Из выражения (5.18) следует, что при фиксированном значении ох логарифмическая функция правдоподобия максимальна, если ми-

П

нимальна сумма ^ (х> — тх)2- Этот факт положен в основу частного і=і

случая метода максимума правдоподобия — метода наименьших квадратов.

В общем виде, если имеется функция у = (р(х, си, а2, …, ah), завися­щая от аргумента х и постоянных параметров аь а2, …, ак, и если в ре­зультате испытаний получены п наблюдений (щ, x-L при і = 1,2, …,

XX /X /X

п), можно найти такие оценки а2, …, ah, при которых

" л л л а

— In LH. K == 2j Уі — Ф (хі> «і. а2……… «*)] = min. (5.23)

t=i

Если значения у; распределены нормально, величины хь измеряют­ся в опыте без ошибок (детерминированы) и функция ср(х, си, аг, …. а,.)

линейна, то оценки oi, а2, …, ah, определенные по методу наименьших квадратов, совпадают с оценками максимального правдоподобия.

При отсутствии перечисленных условий часто используют метод наименьших квадратов, так как вычисление оценок по (5.23) значитель­но проще, чем нахождение оценок максимального правдоподобия, при этом эффективность и смещенность оценок, найденных по методу наименьших квадратов, остаются приемлемыми.

Э|п’-н. eta*

Чтобы вычислить оценку методом наименьших квадратов, необхо­димо минимизировать непосредственно функцию (5.23) или решить систему так называемых нормальных уравнений (полагаем, что функ­ция (5.23) имеет один минимум]:

Если функция ф(х, аи а2, …, ak) описывает прямую линию, т. е. Ф(х, а.1, аг, …, ак) = ах + Ь, то система (5.24) сводится к двум урав­нениям. Действительно, функция (5.23) принимает вид

П

In Д,.к — 2 (уі — axt — bf,

і=і

а нормальные уравнения после элементарных преобразований записы­ваются следующим образом:

П п

2 (Уі — Щ — b) xt = 0; 2 (У і — aXi — b) = 0. (5.25)

і~ t—1

Наконец, при b — 0 (прямая у — ах + b проходит через начало

координат) остается только первое уравнение системы (5.25), которое можно записать в виде

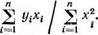(5.26)